Turns out I'm just as comfortable with geeks, as I'm comfortable talking to entrepreneurs :) The 15th and 17th of this month witnessed a conference on Formal Methods in various sectors of software programming. This was the first workshop the Computer Society of India conducted in India, on the formal methods; at IISc Bangalore (some more info about the institute here).
 |
| The stately IISc main building |
 |
| The lush green campus at the IISc |
The Computer Society of India was established in 1965. The Bangalore chapter is the 7th in India. It has 2700 members, 72 chapters and 600+ student chapters.
After the inauguration ceremony...
...we were introduced to the problems researchers face when they try to introduce Formal Methods to the industry. The only thing the industry is interested in, is in profits and product-performance. So if you try to introduce formal methods anywhere, you'll face resistance because of its complexity and time-consuming nature. How do you feed it to the industry then? You sugar-coat it.
Topics
- General info on Formal Methods (Dr.Yogananda Jeppu)
- Deductive verification of C programs (Dr.Kalyan Krishnamani)
- Refinement based verification and proofs of functional correctness (Prof. Deepak D'Souza)
- An industry perspective on certifying safety critical control systems (Dr.Yogananda Jeppu)
- Race detection in Android applications (Prof. Aditya Kanade)
- Probabilistic programming (Dr.Sriram Rajamani)
- Statistical model checking (Prof.Madhavan Mukund)
- Formal methods and web security (By Prof. R.K.Shyamsundar)
- Architectural semantics of AADL using Event-B (Prof.Meenakshi D'Souza)
General info on Formal Methods
By Dr.Yogananda Jeppu (Moog India)
Dijkstra said "Program testing can be used to show the presence of bugs, but never to show their absence!". Being 99% safe is not sufficient for a safety-critical system. Ideally, programmers shouldn't waste their time debugging; they shouldn't introduce a bug in the first place.
The very first build that Dr.Yogananda's team did on the LCA's code, they found a divide-by-zero error. He says it happens often in flight-critical code. It has even caused a ship to get stranded at sea. The whole control system failed and they had to lug the ship with another ship. Imagine what would have happened if it was war-time.
So why do bugs exist and what can be done about it?
It happens because of the language we write requirements in - "English". English sentences can be interpreted in many ways. People misunderstand requirements simply by assuming things. This is where formal methods come in.
We require something more than English to define our system requirements. It's defining a complex system as a mathematical model broken down into little requirements where every requirement has a mathematical equation. Once you define that, it becomes easy for us to prove (using provers) that the system behaviour is right.
Formal methods aren't new. There were papers written on it in 1969 and 1975. There is a set of formal specifications where you write the requirements in a modelling language (perhaps a Z-language). The engineer works with a set of theorems. Eg: one of the theorems could be that you turn on a switch, electricity flows and a bulb should glow. But when you do the theorem proving, you'll find out that the bulb is fused and the light won't turn on. That's when you realize that it's something you missed mentioning in your theorem condition. Such proofs will come up when you try to prove conditions in a formal notation.
So we write an equation, run it and re-define the system behaviour. That's how formal methods are used. After that it's just a question of writing this mathematical equation in C code, compiling and running it.
- Specify your system
- Verify your system
- Generate your code
- And you're ready to fly! (it's not so easy though)
Non-acceptance of formal methods and semi-formalizing it
When testing is too difficult and if formal methods are not accepted in the industry due to complexity or a time-crunch, a lighter version of formal methods can be used - maybe just assertions, just a mathematical equation or for some part of the system you could use formal methods. For the Saras aircraft, they did mode transitions in a semi-formal way. Airbus is using it for low-level testing to check for the highest value of the integer or float or a worst case timing analysis. You can qualify the tool for checking such parameters.
Given that the DO-178C certification is necessary for avionics, there's a formal methods component released in Dec 2011 which can be used to comply with the certification requirements. Expressing requirements in the form of mathematics forces the person to ask questions and clarify the requirements.
Deductive verification of C programs
By Dr.Kalyan Krishnamani (NVIDIA)
Wikipedia defines deductive verification as "...generating from the system and its specifications (and possibly other annotations) a collection of mathematical proof obligations, the truth of which imply conformance of the system to its specification, and discharging these obligations using either interactive theorem provers (such as HOL, ACL2, Isabelle, or Coq), automatic theorem provers, or satisfiability modulo theories (SMT) solvers".
Deductive verification can be performed using Frama-C. It has a bunch of plugins for value analysis (what values the variables of a program can take to compute), coverage and other method plugins. You can write your own plugins too (like one to detect divide by zero). Plugins are written in the OCaml language (it's easy to learn, but writing optimal code in it is an art).
Why verification?
In 1996, the Ariane 5 rocket crashed because they used the same software as the previous generation rocket (they didn't bother to verify it), and while trying to convert a 64 bit int into a 16 bit int, the software shutdown due to an overflow error. The rocket had a backup software, in case the first software shutdown because of an error, but the backup software was the same thing, so that also shutdown and the rocket disintegrated (that's what rockets are programmed to do if something goes wrong).
That was long ago, but even today, verification methods are needed. More so, because software complexity has increased. Airbus and Dassault aviation use Frama-C (Framework for Modular Analysis of C programs) very often.
What it does: Frama-C gathers several static analysis techniques in a single collaborative framework. The collaborative approach of Frama-C allows static analyzers to build upon the results already computed by other analyzers in the framework.
You can verify functions standalone. You don't need a main() function. It uses CIL (C Intermediate Language). It also uses ACSL (ANSI C Specification Language) as the front-end.
This is how verification would be done with ACSL, for a function that returns the maximum value of two values (the code in comments is the verification code. Note how it checks to ensure that the return value should be either x or y and no other number. Would you have checked for this condition if you wrote a test case?):
/*@ ensures \result >= x && \result >= y;Once a programmer defines such conditions, you don't need to do any documentation. The ASCL notation itself becomes the document/requirement specification for the next person who comes across the code. There's no miscommunication either, since it's mathematically expressed.
ensures \result == x || \result == y;
*/
int max (int x, int y) { return (x > y) ? x : y; }
Through ASCL, you can use annotations, named behaviours, allocations, freeable, ghost variables, invariants, variant and inductive predicates, lemma, axiomatic definitions, higher-order logic constructions, lambdas and more.
Frama-C can also be used for regular testing, using plugins.
The architecture
As shown in the image below, the tool Krakatoa (which processes Java programs through the Why 2.30 tool) is the predecessor to Frama-C for Java (KML (Krakatoa Modelling Language) is the language used for writing the cide properties). These properties are fed into the Why tool and Why converts these properties into an intermediate language, Jessie (although now-a-days, a tool called WB is used instead of Jessie). Why then works on what Jessie generates and then Why generates Verification Conditions (VC). It's a bunch of assertions like mathematical formulae which will be translated to the various prover modules. Encoding (rather call it 'translator') takes the verification conditions and translates it into the different input languages for the provers. So if the verification conditions are satisfied, the properties (specification) you wrote are correct.
 |
| Architecture of certification chains: Frama-C, Why, Why3 and back-end provers |
- For Frama-C, the input is a C program.
- Deductive verification (the technique which, through a bunch of rules generates the VC's) generates the verification condition (so you don't even need to know deductive verification to start using Frama-C. You'll need to know a bit of Jessie though, when you need to debug).
- Then, provers like Simplify are then used to verify it.
For arrays, structures, unions etc., Frama-C already provides the commonly used memory models. It allows you to also specify your own memory model and also allows you to download any other model and integrate it with your system. They needed to introduce the feature of downloading any other module, because the next version of Frama-C might support C++.
Hoare's triple
Deductive verification research is based on the Hoare's triple. You have a set of rules. The rules will dictate how to handle a variable assignment, how to handle a loop and so on.
This is the Hoare's triple: {P} s {Q}
Where s can be any program fragment (if statement etc.). P is the pre-condition, Q is the post condition (P and Q are the pre and post conditions that the user writes; remember ASCL above?). If P holds true, Q will hold true after the execution of s.
Other tools
While Why is an excellent tool for a modelling or verification environment, other tools like B-method (used in the automotive industry), Key (used for Java deductive verification of the Paris automated metro trains. It generates loop invariants automatically), Boogie, Dafny, Chalice (for deductive reasoning) and COMPCERT (This tool can actually replace GCC. It's a certified C compiler which caters to strict coding guidelines which are necessary for avionics softwares. Eg: variables can't be used without first initializing them) are also helpful. Frama-C is not just a Formal tool. There are also coverage tools (for unit testing), Runtime error checking, data flow analysis and plugins for concurrent programs and more.
To know which tool is best suited to what application/field, ask the researchers who work in that field.
Refinement based verification and proofs of functional correctness
By Prof. Deepak D'Souza (IISc)
Prof. Deepak introduced us to the question of "How do you prove functional correctness of software?"
If you were to verify the implementation of a queue algorithm, one way to prove it is to use pre and post conditions. The other way is to prove that the implementation refines (provides the same functionality as) a simple abstract specification.
Hoare logic based verification can prove complex properties of programs like functional correctness and thus gives us the highest level of assurance about correctness (unlike testing techniques which do not assure us of a lack of bugs). The graph below shows the level of correctness that's required and the amount of correctness that's provided by the four techniques.
In the picture above, Frama-C is what uses an abstraction refinement technique, whereas bug detection is the normal testing done with ordinary testing tools.
Hoare's logic was checked using the VCC tool. For the max() function similar to what was proved using Frama-C, the logic here is written in VCC with this kind of syntax:
int max(int x, int y, int z)
_(requires \true)
_(ensures ((\result>=x) && (\result>=y) && (\result>=z)))
Again, there's another condition to be added here, which has to ensure that the result returned should be either x, y or z, and not any other number.
The condition is then sent to an SMP (Shared MultiProcessor) solver which says whether the condition is true or not.
Overall strategy for refinement
To verify a program, you have to use both techniques. First, Hoares technique where you use refinement language to generate annotations and then use the annotations in tools like Frama-C. Both techniques have to be used for verifying a program.
An industry perspective on certifying safety critical control systems
By Dr.Yogananda Jeppu (Moog India)
This talk was about mistakes we make in safety critical applications.
What is a Safety Critical Application? When human safety depends upon the correct working of an application, it's a safety critical application. Examples: Railway signalling, nuclear controllers, fly-by-wire, automotive domain (cars have more lines of code than fighter jets), rockets, etc.
Every industry has its own standard for safety (avionics, railways etc.). But accidents still happen and safety problems can cause products to be recalled (like Toyota which had a software problem which prevented the driver from applying from the brakes).
Dr.Yogananda proceeded to show us many examples of past incidents were shown, of how aircraft crashed because of software errors that showed the plane's elevation wrongly, people being exposed to too much radiation in a medical system because of a software error (in 2001 and 2008 which shows that programmers make the same mistakes repeatedly), trains crashing into each other due to sensors erroneously reporting that the trains were not in each others path.
In hindsight, all these errors could have been caught by the one test case that was not written. Fault densities of 0.1 per 1000 lines of code are experienced in space shuttle code. In the nuclear industry, the probability of an error is 1.14*10E-6 per hour of operation (what it actually should be is 10E-9 or lower, but the industry is nowhere near that).
Dormant errors
Once, an error of a tiny number; 10E-37 was found in an aircraft software after it lay dormant for twelve years. This was due to denormal numbers; the fact that floating numbers can be represented upto 10E-45 in PC's, but in some compilers numbers smaller than 10E-37 are treated as zero. So in one of the aircraft channels, the number was 10E-37 and in the other it was 10E-38. So one channel didn't work properly and the issue came to the forefront when an actuator had issues in a certain unique situation. Note that this happened after all the flight testing happened. Errors in filters and integrator systems are common in missile systems and avionics.
So code coverage tests are very important. Also check variable bounds by running many random cases and monitor the internal variables and collect max and min values. Formal method tools are there to do this. Many times, designers don't take verifiers observations into account. They say it's not necessary and talk about deadlines. Never generate test cases just to achieve code and block coverage. They only show locations of the code that aren't tested. They don't show deficiencies.
Nothing is insignificant in safety critical applications.
Standards
You have to know what kinds of problems can happen in a system before writing code. Standards help with this. The aerospace industry has standards like the D0178B. Coding takes just about quarter the time that verification takes, but verification is very necessary. Certification is a legal artefact that has to be retained by a company for 30+ years.
Model based testing and logical blocks
You can even use Microsoft Excel based equations as a model for testing. If model and code outputs match, we infer the code is as per requirements. Instrumented and non-instrumented code output should match very well with model output. You cannot rely on a tool that generates test cases.
For safety critical application, all logical blocks have to be tested to ensure modified condition / decision coverage (MC/DC).
Orthogonal arrays
Orthogonal arrays can be used in any field to reduce the number of tests. A free software for this is called "All Pairs". MATLAB has orthogonal array generation routines. Also, ACTS tool from National Institute of standards and technology called SCADE can help with certification.
Any safety critical tool has to be qualified. It's not an easy task and you shouldn't use a software without it being qualified for use. Hire someone to qualify it and test the limitations of the tool under load.
Testing tantra
- Automate from day one.
- Analyze every test case in the first build.
- Analyze failed cases. Do a debug to some level.
- Eyeball the requirements.
- Errors are like cockroaches. You'll always find them in the same place (cockroaches are always found behind the sink). Eg: you'll always find problems with variable initialization.
- It's useful to have a systems guy close-by.
- Have tap out points in model and code.
Race detection in Android applications
By Prof. Aditya Kanade (IISc)
This talk was about formalizing concurrency semantics of Android applications.
Algorithms to detect and categorize data races and Environment Modeling to reduce false positives.
Droid racer is a dynamic tool developed by Prof. Aditya's team, to detect data races. It runs on Android app's and monitors the execution traces to find races in that execution. They have run it on applications like Facebook, Flipkart and Twitter, and found data races. It performs systematic testing and identifies potential races in popular apps.
The Android concurrency model
Dynamic thread creation (forking), locking, unlocking, join, notify-wait.
Android has an additional concept called asynchronous constructs: Tasks queues which start asynchronous tasks. Threads are associated with task queues. Also called event driven programming. A FIFO model, where any thread can post an asynchronous task to the task queue.
Eg: While you're playing a game on your phone, an SMS might arrive or your battery may go low and the phone would give you a warning message.
Atomic execution of asynchronous tasks takes place. There's no pre-emption. Once a thread is assigned a task, the task is run to completion.
 |
| A typical Android thread creation and destruction sequence |
Android can also have single threaded race conditions.
Sources of non-determinism can be:
- Thread interleaving
- Re-ordering of asynchronous tasks
When checking for races you have to check for:
- Forks happening before initialization of newly forked thread
- Thread exits before join
- Unlock happening before a subsequent lock and more
Droid Racer algorithm
It uses a graph of vertices and edges which creates what the professor refers to as a "happens-before ordering". To check for problems, they do a depth-first-search to pick two memory locations and check if they share an edge in the graph. If there's no edge, you've found a data race.
Data races are classified into...
...multi-threaded (non-determinism caused by thread interleaving)
and
Single-threaded data races. They can be...
- co-enabled (where high level events causing conflicting operations are un-ordered)
- cross-posted (non-deterministic interleaving of two threads posting tasks to the same target thread)
- delayed (at least one of the conflicting operations is due to a task with a timeout. This breaks FIFO)
 |
| These were the data races they found in some popular applications |
Droid Racer is available for download from the IISc Droid Racer website.
Probabilistic programming
By Dr.Sriram Rajamani (Microsoft)
Probabilistic programs are nothing but C, C#, Java, lisp (or any other language) programs with...
1. The ability to sample from a distribution
2. The ability to condition values of variables through observations
The goal of a probabilistic program is to succinctly specify a probability distribution. For example, how are chess players skills modelled in a program?
The program looks like this:
float skillA, skillB, skillC;
float perfA1, perfB1, perfB2,
perfC2, perfA3, perfC3;
skillA = Gaussian(100, 10);
skillB = Gaussian(100, 10);
skillC = Gaussian(100, 10);
// first game: A vs B, A won
perfA1 = Gaussian(skillA, 15);
perfB1 = Gaussian(skillB, 15);
observe(perfA1 > perfB1);
// second game: B vs C, B won
perfB2 = Gaussian(skillA, 15);
perfC2 = Gaussian(skillB, 15);
observe(perfB2 > perfC2);
// third game: A vs C, A won
perfA3 = Gaussian(skillA, 15);
perfC3 = Gaussian(skillB, 15);
observe(perfA3 > perfC3);
return (skillA, skillB, skillC);
Skills are modelled as Gaussian functions. If player A beats players B and C, A is given a high probability. But if player A had beaten player B and then B beats A in the next game, we assume a stochastic relation between the probability and A's skill (which means that the program will be unsure and assign a probability which will not be too high on the confidence of whether A's skill is really good. Pretty much like how our brain thinks). Now if A beats C, then A gets a better rating but still there's a lot of flexibility in whether A is really better than B or not.
Ever wondered how scientists make predictions about the population of animals in a forest or calculate the probability that you'll be affected with a certain disease etc.? The Lotka Volterra population model is used here. It can take into account multiple variables for calculation and prediction. Well known models are that of the calculation of the population of goats and tigers in a forest, calculation of the possibility of kidney disease based on age, gender etc., hidden Markov models for speech recognition, Kalman filters for computer vision, Markov random fields for image processing, carbon modelling, evolutionary genetics, quantitative information flow and inference attacks (security).
Inference
Inference is program analysis. It's a bit too complex to put on this blog post, so am covering this only briefly.
The rest of the talk was about Formal semantics for probabilistic programs, inferring the distribution specified by a probabilistic program. Generating samples to test a machine learning algorithm, calculating the expected value of a function with respect to the distribution specified by the program, calculating the mode of distribution specified by the program.
Inference is done using concepts like program slicing, using a pre-transformer to avoid rejections during sampling and data flow analysis.
Statistical model checking
By Prof. Madhavan Mukund (CMI)
Model checking is an approach to guarantee the correctness of a system.
The professor spoke about stochastic systems where the next states depend probabilistically on current state and past history. Markov property and probabilistic transition functions.
Techniques for modelling errors
- Randomization: Breaking symmetry in distribution algorithms
- Uncertainty: Environmental interferences, imprecise sensors
- Quantitative properties: Performance, quality of service
A simple communication protocol analysed as a Discrete Time Markov Chain
Consider a finite state model where you're trying to send a message across a channel and it either fails or succeeds.
The matrix P shows the probability of going from state to state in a finite state model. Every row adds to 1. The labels {succ} (meaning 'success') are label states with atomic propositions.
We're interested in:
- Path based properties: What's the probability of requiring more than 10 retries?
- Transient properties: What's the probability of being in state S, after 16 steps?
- Expectation: What's the average number of retries required?
Each set of paths can be measured. The probability of a finite path is got by multiplying the probabilities
A single infinite path has a probability of zero.
This way you can model and measure paths that fail immediately, paths with at least one failure, paths with no waiting and at most two failures etc.
Disadvantage of the stochastic method
- Probabilities have to be explicitly computed to examine all states
- You have to manipulate the entire reachable state space
- It's not feasible for practical applications
This approach simulates the system repeatedly using the underlying probabilities. For each run, we check if it satisfies the property. If c of N runs are successful, we estimate the probability of the property as c/N. As N tends to infinity, c/N converges to the true value.
The statistical approach helps, because simulation is easier than exhaustively exploring state space. It's easy to parallelize too. You can have independent simulations. The problem is that properties must be bounded (every simulation should operate within a finite amount of time), there can be a many simulations and the guarantees are not exact.
Monte Carlo model checking
This is performed using a Bounded Linear Time Logic as input and assuming a probabilistic system D. A bound t is computed, the system is simulated N times, each simulation being bounded by t steps and c/N is reported, where c is the number of good runs.
Hypothesis testing
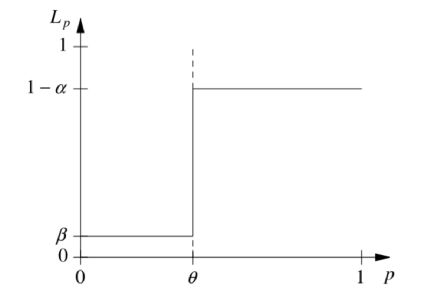
In this technique, we define the problem as P(h) >= θ, call this as our hypothesis H, fix the number of simulations N and a threshold c.
Also have a converse hypothesis K where P(h) < θ.
After the simulation if more than c simulations succeed, accept H. Else accept K.
The possibility of errors are either a false negative (accept K when H holds and the error is bounded by α) or a false positive (accept H when K holds and the error is bounded by β).
This is the extensive sampling method which is not very practical. A better way to do it is shown in the graph below - by considering values from p1 to p0. It's the probability of accepting hypothesis H as a function of P with an indifference region.
Challenges for statistical model checking
- If the probability of an event is very low, we need more samples for a meaningful estimate
- Incorporating non-determinism is difficult because each action determines a separate probability distribution (as in the Markov Decision Process)
Formal methods and web security
By Prof. R.K.Shyamsundar (TIFR)
Information flow control is an important foundation to building secure distributed systems. I asked the professor about this, and he said that to implement this, you need an operating system which is capable of categorizing information packets as secure/trusted/untrusted etc.
Multi Level Security
Sensitive information is disclosed only to authorized persons. There are levels of classification and levels form a partially ordered set.
In an information system, the challenge is to build systems that are secure even in the presence of malicious programs.
There are two aspects to this: Access control and correct labelling of information packets (determining the sensitivity of information entering and leaving the system).
The Bell LaPadula Model
In this model, entities are files, users and programs.
Objects are passive containers for information.
Subjects are active entities like users and processes.
Untrusted subjects are assigned a label. They're permitted to only read from objects of a lower or equal security level.
Trusted processes are exempted from the requirements of the process.
Information Flow Control
This is mandatory for security. Confidentiality and integrity are information flow properties. Security is built into the design and you need to provide an end to end security guarantee.
Labels are assigned to subjects and objects. Read-write access rules are defined in terms of can-flow-to relation on labels.
Lattice model
A lattice is a finite ordered set with a least upper bound and lower bound. Using it, you can define reflexive, aggregation properties etc. It's suitable for any system where all classes need to be totally ordered.
The Biba model
Information can flow from a higher integrity class to a lower integrity class. It restricts a subject from writing to a more trusted object. La Padula is for information confidentiality (prevention of leakage of data).
Biba emphasizes information integrity (prevention of corruption of data).
Protecting privacy in a distributed network
This involves a de-centralized label model. Labels control information flow.
Trusted execution model: Enforcing data security policy for untrusted code. Eg: How do you know if your secure information isn't being transmitted outside by the antivirus program you installed?
In 1985, the Orange Book defined trusted computer system evaluation strategy.
The flaw of older systems were that they considered confidentiality and integrity to be un-related. Downgrading being un-related to information flow control was also a flaw.
Readers-writers labels: Uses the RWFM label format.
State of an information system: It's defined by subjects, objects and labels.
Downgrading does not impact ownership, but you are giving read access to others. It's easy to verify/validate required security properties.
Application security protocols: There are authentication protocols and security protocols for this. Eg: The Needham Schroeder Public Key Protocol implemented in Kerberos.
Also have a look at Lowe's attack on NSP.
Web security
For cross-origin requests (Eg: a computer accessing Gmail and youtube at the same time), one of the major problems is in inaccurately identifying the stakeholders.
Architectural semantics of AADL using Event-B
By Prof. Meenakshi D'Souza (IIIT-B)
The Architecture Analysis and Design Language is used to specify the architecture of embedded software. This is different from a design language. It speaks of components and how they interact.
Consider the cruise control system of a car:
 |
| Abstract AADL model |
AADL allows modular specification of large-scale architectures.
The architecture specifies only interactions. Not algorithms. AADL gives mode/state transition specification system. It allows you to specify packages, components, sub-components etc.
- AADL lets you model application software (threads, processes, data, subprograms, systems), platform/hardware (processor, memory, bus, device, virtual processor, virtual bus)
- Communication across components (data and event ports, synchronous call/return, shared access, end-to-end flows)
- Modes and mode transitions
- Incremental modelling of large-scale systems (package, sub-components, arrays of components and connections)
- There's an Eclipse-based modelling framework, annexes for fault modelling, interactions, behaviour modelling etc.
Will you be able to use a formal method to check the property templates of AADL?
You have to. Because it has to be automated. AADL can't check an end-to-end latency on its own.
A formal method is needed. Same for bandwidth of the bus (in the diagram).
Event B
It's a formal modelling notation based on first order logic and set theory. Refinements in Event-B are formalized.
Dynamic behaviours are specified as events.
The Rodin toolset has a decomposition plugin which breaks down a machine into smaller machines/components.
The number of proof obligations is huge in Event B for just a small set of AADL flows.
This is what an Event B program would look like:
This is how AADL is converted to Event B
Proving of architectural properties:
First, an Event B model corresponding to AADL model of the system is arrived at with manual translation.
The AADL model includes the system, devices, processes, threads, modes, buses, timing properties for thread dispatch, transmission bound on buses.
Global variables model the time and timing properties of threads in Event B.
End to end latency requirement of AADL is specified using a set of invariants of the overall model.
Correct latency requirements are discharged through 123 proof obligations, few of which are proved through interactive theorem proving.
Conclusion
It's possible to provide semantics of architectural components in AADL using Event-B. Such semantics will help designers to formally prove requirements relating to architecture semi-automatically. Professor Meenakshi's team is currently implementing a translator that will automatically generate and decompose incremental Event B models from incremental AADL models.











No comments:
Post a Comment